https://arxiv.org/abs/1708.00489
Active Learning for Convolutional Neural Networks: A Core-Set Approach
Convolutional neural networks (CNNs) have been successfully applied to many recognition and learning tasks using a universal recipe; training a deep model on a very large dataset of supervised examples. However, this approach is rather restrictive in pract
arxiv.org
1. Introduction
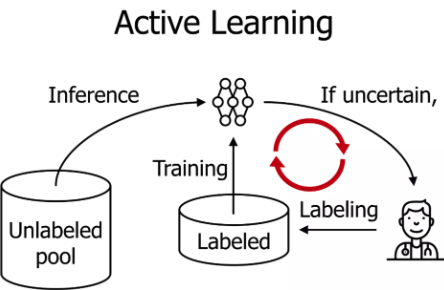
Active Learning?
model이 원하는, 배우고 싶은 데이터를 선택하여 적은 학습으로 좋은 성과내도록 하는 방법
unlabeled data에서 annotation effort를 줄이는 방법
pretrained model이 inference를 하는데 불확실한 데이터에 대해서만 사람이 labeling
unlabelled data를 활용하는 방법 중 하나라고 생각하면 됨
기존 AL(active learning 줄여서) 에서는 universal하게 쓰일 수 있는 좋은 전략을 얻는 것은 불가능!
→ heuristic한 많은 방법론만 존재 → but CNN에 적용 했을 때는 효과적이지 않음…
저자들은 주요 이유로 batch acquisition/sampling에서 발생하는 correlation때문이라고 함
why? AL의 classical setting을 보자
⇒ 각 iteration에서 single point 하나를 선택하는 것이 위주
그러나 CNN에는 이러한 방식이 적합하지 않음
- single point는 accuracy에 큰 영향을 끼치지 않음
- 각 Iteration에서 수렴할 때까지 full training → label을 하나하나 추적하기 어려움
⇒ CNN에서는 각 iteration 마다 큰 subset(batch)을 query ⇒ correlation 발생
저자들이 제시하는 방법 : core-set selection problem
<aside> 💡 larged dataset에서 전체 dataset에 대해 경쟁력있는 small subset 찾는 것이 목표
</aside>
그리고 이 subset에 대한 average loss와 data points의 기하학적 구조를 통해 남아있는 data point와의 엄격한 경계를 제시?? ⇒ 그리고 이 bound를 최소화 하는 subset을 선택하기 위한 algorithm
2. Problem Definition
large data space : $\mathcal Z = \mathcal X \times \mathcal Y$ ($\mathcal X$ : compact space, $\mathcal Y$: label space)
$\mathcal Z$ data points : $\{x_i, y_i\}{i\in[n]} \sim p\mathcal Z\qquad \text{where} [n] = \{1, ..., n\}$
초기에 uniformly random하게 선택된 data points $s_0 = \{s^0(j)\in[n]\}_{j \in [m]}$
AL은 $\{x_i\}{i\in ]n]}$ , $\{ y{s(j)}\}_{j\in[m]}$에만 접근 ⇒ 즉, 초기 data pool에 존재하는 points의 label만 볼 수 있음!
b : oracle(사람)에게 물어볼 query budget, $A_s$ : 주어진 labelled set s에 대해 parameter $\mathbf w$ 반환 알고리즘
⇒ active learning이 다음과 같이 정의됨
$$ \min_{s^1:\vert s^1 \vert \le b} E_{x, y \sim p_\mathcal z}[l(x, y;A_{s^0\cup s^1})] $$
즉, 최대 b개의 추가 points를 선택하고 이들을 oracle에 의해 라벨링 하여 expected loss를 최소화 한다
classical 방식은 무조건 b=1 하지만 앞에서 말했듯이 이는 deep learning에서는 의미 x
각 iteration마다 두가지 단계를 거침
- 몇몇 data-points 뽑기 → oracle에 labelling 요청
- 새롭게 라벨링된 data들과 기존 라벨링 된 data 같이 이용해 classifier 학습(fully-or weakly-둘다가능)weakly : 아직 labelling되지 않은 data도 같이 이용(semi)
- fully : labeling된 data point만 이용
방법론 설명은 fully로 focus하고 결과는 둘다 보여줌
3. Method
3.1 Active Learning as a Set Cover
active learning loss식을 살펴 보자
$$ E_{x, y \sim p_\mathcal z}[l(x, y;A_s)] \le \left| E_{x, y \sim p_\mathcal z}[l(x, y;A_s)] - {1\over n}\sum_{i \in [n]}l(x_i,, y_i;A_s)\right| + {1\over \vert s \vert}\sum_{j\in s}l(x_j, y_j;A_s) + \left|{1\over n}\sum_{i \in [n]}l(x_i,, y_i;A_s) - {1\over \vert s \vert}\sum_{j\in s}l(x_j, y_j;A_s)\right| $$
왼쪽 두 개 term : Generalization error : 전체 dataset이 model 학습에 어떤 영향을 끼치는가
가운데 term : Training error : 라벨링된 small set이 model 학습에 어떤 영향 끼치는가
오른쪽 두 개 term : Core-set error
core-set error : 전체 dataset에 대한 empirical loss와 라벨링된 data에 대한 empirical loss사이의 차이
경험적으로 Training error는 CNN에서 매우작아 영향 끼치지 않음
Generalization error의 경우 CNN의 뛰어난 성능으로 0으로 설정할수 있다..?
⇒ 결국에 집중해야할 부분은 core-set loss
$$ \min_{s^1:\vert s^1\vert \le b} \left|{1\over n}\sum_{i \in [n]}l(x_i,, y_i;A_{s^0 \cup s^1}) - {1\over \vert s^0 + s^1 \vert}\sum_{j\in s}l(x_j, y_j;A_{s^0 \cup s^1})\right| $$
⇒ labelled set으로 학습 했을 때 성능이 전체 dataset으로 학습 했을 때와 가능한한 비슷하도록
이 논문에서는 k=1 의 경우를 위주로 보며 당연하게 매 라운드마다 라벨링을 한다고 생각하면 됨
⇒ 주어진 초기 라벨링된 set($s^0$)와 budget(b)이 있을 때 query할 label set($s^1$) 찾는 문제
3.2 Core-Sets for CNNs
우리가 집중할 loss 식을 보았을 때 계산 가능해 보일까? no
why? ⇒ 왼쪽 term을 봤을 때 우리는 모든 label에 접근할 수 없기 때문($s^0, s^1$만 알고 있음)
⇒ 우리가 optimize할 수 있는 upper bound를 찾고자 함
- Lipschitz continuous
- 함수 f에 대해 ${\left| f(x_1) - f(x_2) \right|\over \left| x_1 - x_2\right|} \le K$ 일 때 K-Lipschitz continuous하다고 함
<aside> 💡 Theorem 1
만약 loss function $l(\cdot, y, \mathbf w)$가 모든 $y, \mathbf w$에 대해 $\lambda^l$ - Lipschitz continuous하고, 상한이 L일 때, regression function은 $\lambda^\eta$-Lipschitz이고, s는 data points $\{x_i, y_i\}{i \in [n]}$을 $\delta_s$거리 내에 포함시킴 그리고, 모든 $\forall j \in [m]$에 대해 적어도 $1-\gamma$의 확률로 $l(x{s(j)}, y_{s(j)};A_S) = 0$ 이다.
</aside>
$$ \left|{1\over n}\sum_{i \in [n]}l(x_i, y_i;A_s) - {1\over \vert s \vert}\sum_{j\in s}l(x_j, y_j;A_s)\right| \\ \le \delta(\lambda^l + \lambda^\mu LC) + \sqrt{L^2\log(1/\gamma)\over2n} $$
⇒ 다른 data들을 나타낼 수 있는 최적의 거리 $\delta_s$를 구하고, 그에 맞는 core point s(다음 section)를 찾는다
이전에 training error를 0으로 설정 따라서 average error로 쉽게 표현
$$ \left|{1\over n}\sum_{i \in [n]}l(x_i, y_i;A_s) - {1\over \vert s \vert}\sum_{j\in s}l(x_j, y_j;A_s)\right| = {1\over n}\sum_{i\in [n]} l(x_i, y_i;A_s) $$
아래 그림으로 visualize(appendix에 증명 존재)

이제 우리가 얻은 bound가 CNN에 적용이 가능한지 살펴볼 예정
CNN에 max-pooling같은 restricted linear unit들과 loss function (여기서는 l2와 cross-entropy), soft-max outputs같은 요소들이 있는데 이런거가 있어도 저 bound가 유지되는지
여기서는 l2 loss에 대해서만 다루고 cross-entropy는 결과로만 제시(성능은 cross-entropy가 더 좋았다고)
<aside> 💡 Lemma 1 C개의 class에 대해 고정된 class probability와 conv($n_c$)+fc($n_{fc}$)로 이루어진 network사이의 l2 loss function은 $({\sqrt {C-1} \over C}\alpha^{n_c + n_{fc}})$-Lipschitz continous하다
</aside>
자세한 증명은 appendix 볼것. 증명 진짜 대박임
3.3 Solving the k-center problem
Core-set (s)를 어떻게 찾냐에 대한 문제 ⇒ K-center problem(2011)방법론 이용
center points 와 가장 거리가 먼 data points($x_i$)와 이 data point와 가장 가까운 core-set point($x_j$)사이 거리를 최소로 하는 것이 우리가 풀어야할 문제
$$ \min_{s^1:s^1\le b} \ \max_i \ \min_{j \in s^0 \cup s^1} \Delta(x_i, x_j) $$
이 문제는 NP-Hard문제로 2-OPT방식으로 해결


이 2-OPT solution을 발전시킴 MIP 방법 이용해서 했다는데 속도가 122배나 느리는데 저자는 쓸만했다고함..
MIP방법에 대한 수식과 알고리즘이 있는데 머리아파서 일단 알고리즘만 올림…속도가 122배나 느리데서 일단은 자세하게는 보진 않을 예정. 필요시 리뷰(이상치에 대한 취약점 커버)
4. Experiments

weakly를 어떻게 학습했는지는 나오지 않음(semi)
Uncertainty vs diversity

전자는 uncertainty를 이용한 al, 후자는 이 논문 방식, 각 data point embedding보면
파란점 : 초기 labelled data
초록점 : al 통해 labeling한 data
빨간점 : 안뽑힌 data
uncertainty는 치우칠 수 있다는 단점이 있는데 이를 해결할 수 있다
Limitation
- boundary 근방의 정보가 취약하다
- data 밀집도에 영향을 받는다
- 이상치에 취약하다
'vision' 카테고리의 다른 글
| DINO : Emerging Properties in Self-Supervised Vision Transformers (0) | 2024.01.12 |
|---|---|
| MAE:Masked autoencoders are scalable vision learners (1) | 2024.01.11 |
| HummingBrid: Towards In-context Scene Understanding (0) | 2024.01.10 |


